선형회귀의 5가지 가정 실습 in R
Linear Regression은 몇 가지 가정과 함께 모델을 만든다. 이번 포스팅에서는 그 가정을 간략히 살펴보고, 데이터와 모델이 가정에 부합하는지 판단할 수 있는 R 코드를 설명한다.
그 가정들은 다음과 같다.
선형회귀모형이 $Y_i = \sum \alpha_i X_i + \beta + \epsilon_i, \epsilon_i \sim N(0, \sigma^2)$ 을 가정한다는 점을 상기하면 이해에 도움이 될 것이다.
1. 선형성: 종속 변인과 독립 변인 사이에 선형적 관계가 존재해야 한다.
당연한 이야기다. Linear Regression이 무엇인지 안다면 자명하게 받아들일 수 있다.
2. 다중공선성 X: 독립 변인들 간의 강한 상관관계가 없어야 한다.
다중선형회귀분석에서만 따져주면 되는 조건이다. 대개의 경우 다중공선성은 중대한 문제로 취급된다. 상관성과는 조금 다른 이야기인데, 상관성이 단순 두 변인 사이를 비교한다면 다중공선성은 여러 변인들 간의 선형관계를 의미한다. 즉 한 독립변인을 다른 독립변인으로 설명할 수 있는 경우다. 자세한 설명은 추후 Theory 카테고리에 첨부하겠다.
3. 자기상관성 X: 서로 다른 두 시점의 관측치(값) 간 상관관계가 없어야 한다.
시계열 데이터에만 해당하는 이야기로, 다중공선성과 비슷한 맥락이다. 다중공선성은 Feature의 독립성이고 자기상관성은 target의 독립성이다. 그래서 2와 3을 합쳐 독립성으로 부르기도 한다.
4. 등분산성: 잔차(residual)는 등분산이어야 한다.
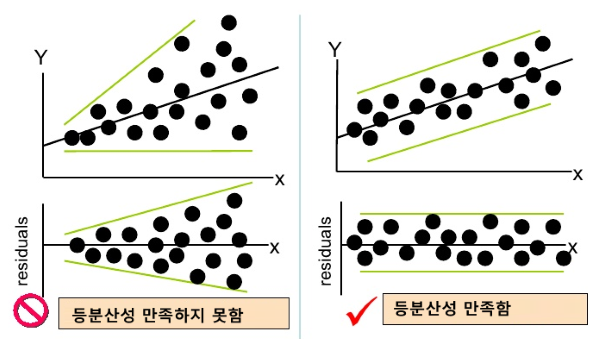
잔차, 등분산에 대해 각각 간략히 설명하겠다. 잔차는 오차(error)와 거의 비슷한 의미다. 모집단으로 만든 모델의 예측값과 실제 값의 차이를 오차, 표본집단으로 만든 모델의 예측값과 실제 값의 차이를 잔차라고 한다. 이 잔차의 값이, 그 예측값의 크기와 상관없이 유사한 산포도로 분포해야 한다. 이를테면 다음과 같다.
종속변인의 크기가 커질수록 잔차의 범위가 커지므로 등분산성을 나타내지 않는다.

5. 정규성: 잔차들은 정규분포를 따라야 한다.
정규성이 무엇인지는 다들 알리라 생각한다.
이 가정을 수학적으로 분석한 글을 추후 theory 카테고리에 올리겠다.
가정 확인법
1. gvlma package
library(gvlma)
summary(gvlma(fit.lm))fit.lm은 선형 회귀 모델로, 본인의 모델을 사용하면 된다. 필자의 경우 필자가 대회를 위해 수행한 설문 조사의 데이터를 사용하고 있다.
gvlma는 비교적 폭넓게 가정 적합성을 알려준다.
ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level of Significance = 0.05
Call:
gvlma(x = fit.lm)
Value p-value Decision
Global Stat 3.916862 0.41737 Assumptions acceptable.
Skewness 0.007034 0.93316 Assumptions acceptable.
Kurtosis 0.004179 0.94846 Assumptions acceptable.
Link Function 3.755001 0.05265 Assumptions acceptable.
Heteroscedasticity 0.150648 0.69792 Assumptions acceptable.summary 결과는 위와 같이 나타난다. 이 해석은 블로그마다 많이 다른데, 오역이 대부분이다.
Global stat: 선형성(종속 변인과 독립 변인들 간 선형적 관계가 나타나는가?)
Skewness, Kurtosis: 왜도와 첨도 -> 잔차의 정규성을 나타내는 지표
Link Function: 종속변인이 정확히 연속형(continuous) 변수인가?
Heteroscedasticity: 이분산성(등분산성의 반의어)
From: https://stackoverflow.com/questions/43252474/using-and-interpreting-output-from-gvlma
Decision을 보면 알 수 있듯이 각 지표의 p-value가 0.05 이상이면 가정에 적합하다고 판정한다.
2. qqplot(정규성 시각화)
qqnorm(fit.lm$residuals)
qqline(fit.lm$residuals)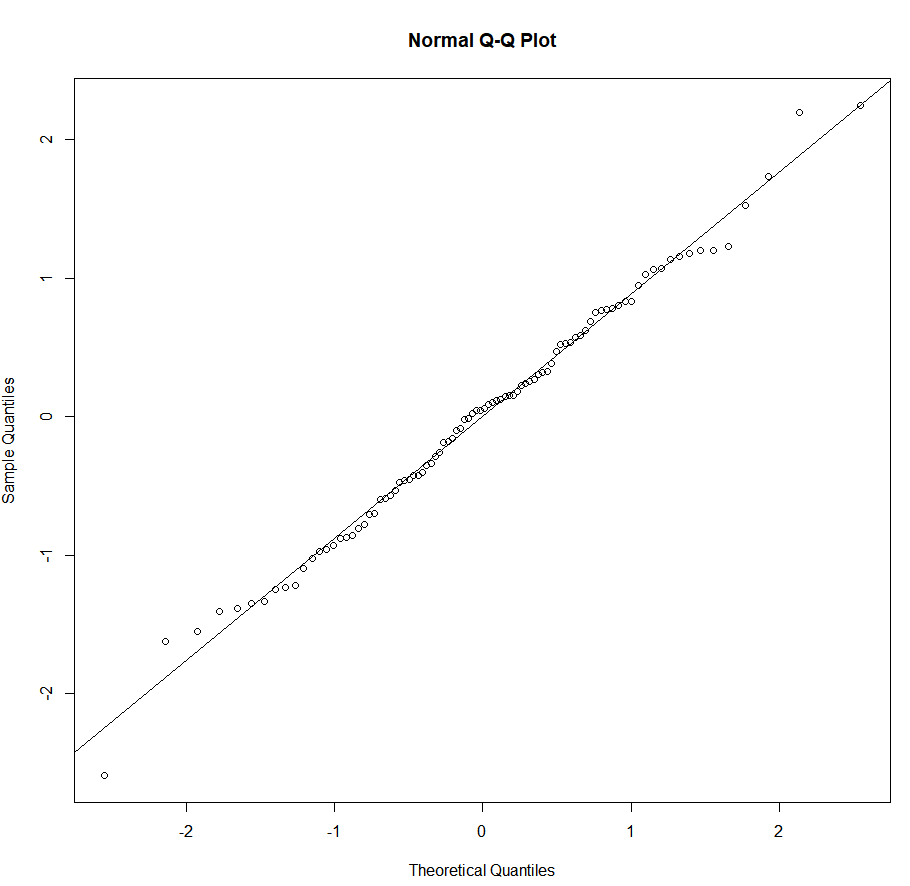
이론적 배경은 생략하겠다. 모델$residuals 로 잔차 데이터를 추출하고, 이를 qqline()으로 plot했을 때 선형성이 잘 나타나면 잔차가 정규성을 나타내는 것이다.
3. Shapiro-Wilk test
마찬가지로 정규성을 검정하는 방법이지만, 정량적인 값이 나오므로 2보다 조금 더 설득력 있다. p-value > 0.05면 정규성을 만족한다고 가정해도 된다. 즉, 이 test에서는 p-value가 높을수록 좋다.
shapiro.test(fit.lm$residuals)Shapiro-Wilk normality test
data: fit.lm$residuals
W = 0.99294, p-value = 0.9104. ncvTest
등분산성을 검정하는 방법이다. p-value > 0.05면 등분산성을 만족한다고 가정해도 된다. 즉, 이 test에서도 p-value가 높을수록 좋다.
library(car)
ncvTest(fit.lm)Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 2.817813, Df = 1, p = 0.093223
5. Durbin-Watson test
자기상관성을 검정하는 방법이다. 다만 한계가 명확해 사용에 주의해야 한다. 관련 링크를 첨부할테니 참고하시길 바란다.
https://freshrimpsushi.tistory.com/1217
더빈-왓슨 테스트 Durbin-Watson Test
회귀분석을 한 이후의 잔차 $\left\{ e_{t} \right\}_{t=1}^{n} $ 가 주어져있다고 하고 $e_{t} := \rho e_{t-1} + \nu_{t}$ 이라 하자. $H_{0}$ : $\rho = 0$ 즉, 잔차끼리 자기상관성을 가지지 않는다. $H_{1}$..
freshrimpsushi.tistory.com
6. VIF test
다중공선성을 검정하는 방법이다.
library(car)
vif(fit.lm)car package의 vif는 GVIF(generalized variance inflation factor), df(number of coefficients in the subset)을 출력한다. 이를테면 다음과 같다. 이때 GVIF^(1/(2*df)) > 2인 독립변인은 다중공선성이 있다고 간주하여, 가장 그 값이 큰 변인부터 하나씩 제거해야 한다. 하나씩 제거하는 이유는 한 변인이 제거됨으로써 다른 변인들의 다중공선성이 감소하기 때문이다.
*만약 VIF 지표만 출력된다면, 10을 넘었을 때 다중공선성이 있다고 판단한다.
GVIF Df GVIF^(1/(2*Df))
Form 9.775312 3 1.462250
Picts 2.945955 1 1.716378
Terrible 2.208814 1 1.486208
Skin 2.670464 1 1.634155
line 3.752867 2 1.391845
Thick 1.174562 1 1.083772
Video 2.519966 1 1.587440
imoge 1.237225 1 1.112306
Title 11.391807 4 1.355421
NewYork 1.874573 1 1.369150
Alphabet 1.225920 1 1.107213
BulWanJeon 1.997763 1 1.413422
Link 1.461031 1 1.208731
실습 글이기 때문에 정확한 이론은 생략하였다. 만약 이론적 배경이 궁금하다면 Theory 카테고리 글들을 참고해주시길 바란다.
*아직까지 관련 이론 글을 포스팅하지는 않았다. 포스팅 후 링크를 첨부할 예정이다.
Written By Killer T Cell