다중회귀분석 실습 in R

다중회귀분석은 말 그대로 여러 개의 독립 변인을 회귀분석하는 것이다. 그러나 단일회귀분석과 달리 분석 과정에 여러 주의해야할 점이 존재한다. 글을 보기 전, 회귀계수와 오차항의 정의 정도는 알아두고 가자. 회귀계수는 위 사진에서 beta들, 오차항은 epsilon이다. 즉 회귀계수의 절댓값이 커질수록 독립 변인이 종속 변인에 미치는 영향은 지대해진다. 

 

R 코드를 보며 차차 정리하겠다. csv는 첨부파일에 올려두겠다.

autompg.csv

0.02MB

car<-read.csv("autompg.csv")
attach(car)

# multiple regression : 1st full model 
model1<-lm(mpg ~ disp+hp+wt+accler, data=car)
summary(model1)

다음과 같이 car dataframe을 만들었다.

model <- lm(종속변인 ~ 독립변인, 데이터) 문법으로 다중회귀분석을 할 수 있다. 이를 summary하면 다음과 같다.

 

Residuals:
     Min       1Q   Median       3Q      Max 
-11.8331  -2.8735  -0.3164   2.4449  16.2079 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) 40.8838025  1.9966258  20.476  < 2e-16 ***
disp        -0.0106291  0.0065254  -1.629   0.1041    
hp           0.0047774  0.0082597   0.578   0.5633    
wt          -0.0061405  0.0007449  -8.243 2.54e-15 ***
accler       0.1722165  0.0976340   1.764   0.0785 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.298 on 393 degrees of freedom
Multiple R-squared:  0.7006,	Adjusted R-squared:  0.6976 
F-statistic:   230 on 4 and 393 DF,  p-value: < 2.2e-16

나머지는 차차 설명하도록 하고, Coefficents를 먼저 본다.

Intercept는 y절편이고, Estimate가 각 독립변인의 회귀계수다. Multiple R-squared이 결정계수, Adjusted R-squared이 결정계수를 보정한 값이다. 각각의 지표에 대한 자세한 설명은 다른 포스팅에서 서술하도록 하겠다. 우선 p-value for t-test-value for t-test가 작을수록 통계학적으로 유의하므로, Pr(>|t|) 수치로 유의성을 따져 Estimate의 신뢰성을 매겨야 한다. 그 뒤 유의하다고 판단된 Estimate의 값으로 종속변인과 독립변인 간 관계를 생각한다.

 

한편, 이 모델에는 직관적으로 문제가 있다. hp는 마력인데, 마력이 증가함에 따라 연비가 감소해야 함에도 불구하고 모델은 마력과 연비에 양의 관계가 있다고 해석하였다. 이것이 바로 추가적인 점검이 필요한 이유다.

 

var1<-c("mpg","disp","hp","wt", "accler" )
pairs(car[var1], main ="Autompg",cex=1, col=as.integer(car$cyl))

이렇게 pairs로 산점도행렬을 그렸을 때 mpg와 hp의 관계에서 두 군집을 발견할 수 있다. 분명히 두 군집 모두 음의 관계를 보임에도 단 하나의 선만으로 이 두 군집을 표현하려다보니 양의 관계가 나타난 것이다. 이를 해결하기 위해서, 두 군집을 분리할 필요가 있다. hp를 50을 기준으로 나눠보자.

car_s1<-subset(car, hp<50)
rf1<-lm(mpg ~ disp+hp+wt+accler, data=car_s1)
summary(rf1)

결과는 생략한다. 

 

한편, 독립변인들의 수가 클 때 회귀 모델에 사용할 독립변인들을 선택해야 하는 경우가 많다. 시간복잡도도 한 이유가 될 수 있고, 설명력이 높지 않은 변인들이 모델의 실질적인 정확성을 떨어뜨리는 경우가 발생하기 때문이다. 

이때 다중회귀모델에서는 보통 3가지 방법을 사용한다. forward selection, backward elimination, stepwise method가 그것들이다. 

 

1. backward elimination

모든 변수에서 가장 통계적으로 유의하지 않은 변수를 하나씩 제거하는 방법이다. 여러 개를 한 번에 제거할 경우 다중공선성에 의해 실제로 통계적으로 유의하지 않은 변수가 유의하다고 판별될 수 있기 때문이다. 그 후 모든 변수가 유의하다고 판별되었을 때 선택을 완료한다.

 

2. forward selection

0개의 독립변인으로부터 시작해 가장 모델의 설명력을 높이는 변수를 추가하다가, 더 이상 설명력을 높일 수 없는 변수만이 남았을 때 선택을 완료한다.

 

3. stepwise method

1, 2보다 이 방법을 강력히 추천한다. backward elimination, forward selection을 모두 수행하며 최적의 그룹을 찾는 방법이다. R에서는 forward selection에서 시작하여 변인들을 조정해간다. 이때 최저 AIC값을 갖는 변인들의 조합을 최종적으로 선택한다. 또는 유의한 변인들만 남기기도 한다. 이는 내부 파라미터 설정에 달려있다. AIC를 간략히 설명하면 아래와 같다. 

 

Akaike information criterion

https://towardsdatascience.com/the-akaike-information-criterion-c20c8fd832f2

 

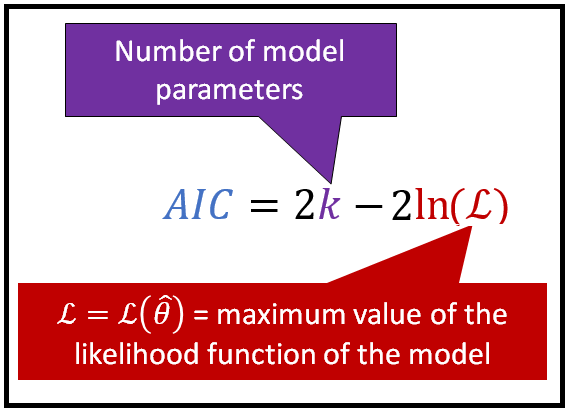
parameter가 적으면 적을수록, likelihood function의 maximum이 클수록 값이 작아진다. 즉 AIC가 작은 모델이 좋다고 생각하면 된다. 

 

R코드는 다음과 같다. 

step(rf1, direction="both")

backward elimination은 direction="backward", forward selection은 direction="forward", stepwise method는 direction="both"를 사용하면 된다.

 

첫 포스팅이라 미숙한 점이 많지만, 팀블로그가 점점 발전할 수 있길 바란다. 다음 포스팅은 선형회귀의 가정을 다룰 것이고, 실제 통계활용대회용 데이터를 사용할 것이다.

 

Written By Killer T Cell