Phylogenetic Tree(계통수) 실습 in R (2) - Neighbor Joining, Maximum parsimony, Maximum Likelihood, Bootstrapping, ggtree

1편에 이어서 글을 작성하겠습니다. 1편 링크 첨부해드립니다.

https://rython.tistory.com/8 

Phylogenetic Tree(계통수) 실습 with R (1) - DNA Alignment, Hierarchical Clustering, Multidimensional Scaling

2편에서는, 1편에서 가공한 데이터와 각종 자료(Clustering) 등을 활용해 phylogenetic tree를 다양한 알고리즘으로 구현하고, 이를 평가한 뒤 ggtree로 시각화할 것입니다. 최종 결과물 먼저 보여드립니다.

 

tree 구현에 앞서 함수 하나를 정의하고 가겠습니다. 구체적인 이론은 향후 xylene님과 함께 포스팅할 예정입니다. R_2 function은 말 그대로 R-squared를 반환합니다. 굳이 이렇게 정의해준 이유는 R에서 지원하는 R-squared가 (pearson coeffiecient)^2을 계산하기 때문입니다! 

R_2 <- function(pred, obs){
  result <- 1 - sum((pred-obs)^2) / sum((obs-mean(obs))^2)
  return(result)
}

 

우선 distance based algorithm 3가지를 살펴보겠습니다. (염기변이를 차이로 생각합니다.)

 

 첫 번째는 UPGMA(Unweighted Pair Group Method with Arithmetic Mean)입니다. 개인적으로 싫어하는 알고리즘입니다. UPGMA는 가장 거리가 가까운 분류군을 cluster로 서서히 묶어나가는 간단한 계층적 clustering 기반 algorithm입니다. 1편에서 서술하였듯 method="average" 방식입니다. 그러나 가중치를 고려하지도 않고, 친연 관계를 오직 거리가 가까운 척도만으로 판단하다 보니 잘못 추론하는 경우가 많이 발생합니다. 

 두 번째는 NJ(Neighbor Joining)입니다. UPGMA의 문제가 많이 개선된 알고리즘입니다. NJ는 단순한 거리 계산뿐만 아니라 트리의 전체 길이를 최소화하는 집합을 탐색합니다. 그러나 long branch attraction이라는 고질적 문제가 있습니다. 간단하게, 실제로는 진화적으로 먼 생명체를 가깝다고 착각하는 오류입니다.

 세 번째는 BIONJ입니다. NJ를 개선한 알고리즘 정도로 생각하시면 됩니다.

 

R 구현은 간단합니다. 저는 이렇게 tree를 만들어주고, root를 설정해주었습니다. root는 1편에서 정했습니다! 만일 1편에서 root를 정하지 못하는 경우라면 아래 링크를 참고해주세요.

http://cabbagesofdoom.blogspot.com/2012/06/how-to-root-phylogenetic-tree.html 

http://phylobotanist.blogspot.com/2015/01/how-to-root-phylogenetic-tree-outgroup.html 

rooting 방법을 알아두시고 phytool package의 midpoint.root function 등을 활용하시면 됩니다.

tree_nj <- nj(distance)
tree_bionj <- bionj(distance)
tree_upgma <- upgma(distance)
tree_nj_rooted <- root(tree_nj, out = "CY013613")
tree_bionj_rooted <- root(tree_bionj, out = "CY013613")
tree_upgma_rooted <- root(tree_upgma, out = "CY013613")

만들어진 tree를 아래와 같이 시각화할 수 있습니다. 저 같은 경우 colour parameter로 clustering 결과까지 tree에 녹여냈습니다.

ggtree(tree_nj_rooted) + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group])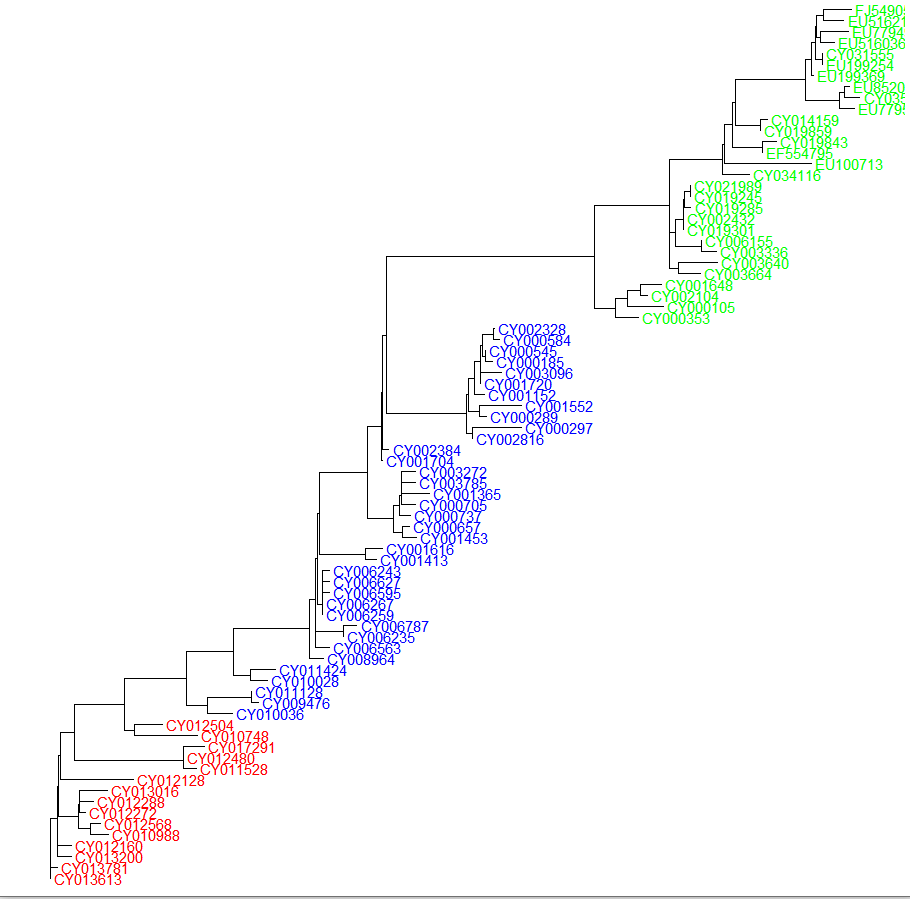

tree_nj_rooted

 그러나 여기서 한 가지 과정을 더 거쳐주는 편을 강하게 권장합니다. 바로 bootstrapping입니다. 이 과정을 통해 phylogenetic tree가 얼마나 안정적인지 판단할 수 있습니다. bootstrap이란 표본을 resampling하여 다시 tree를 만들고, 같은 node가 같은 위치에 발견되는지 검정하는 방법입니다. 즉 안정적인 tree일수록 resampling과 관계없이 node 간 친연 관계가 동일하게 나타날 것이므로, 각 node의 높은 value는 그 node의 안정성을 강력하게 지지하는 지표입니다. 긴말없이 코드로 넘어가겠습니다.

 

 저는 bootstrapping 후 value가 전체의 70% 미만이면 신뢰도가 부족하다고 판단하여 edge.length를 0으로 만들었습니다. 이 과정을 위해 함수를 하나 또 정의하였습니다.

 bootvalue가 stan, 즉 standard보다 낮은 Node의 edge.length를 0으로 만들고 root화한 tree를 반환하는 함수입니다. tree는 phylo 객체, bootvalue는 곧 설명드릴 boot.phylo 함수의 반환 리스트, stan은 70%를 적용했을 때의 값입니다. 향후 더 자세히 서술합니다.

making_boot <- function(tree, bootvalue, stan){
  temp <- tree
  temp$edge
  N <- length(tree$tip.label)
  toCollapse <- match(which(bootvalue<stan)+N, temp$edge[,2])
  temp$edge.length[toCollapse] <- 0
  tree_boot <- di2multi(temp, tol = 0.00001)
  return(root(tree_boot, out = "CY013613"))
}

 또한 tree들을 평가하는 함수를 추가로 정의해주었습니다. 이 함수는 독자들이 자유롭게 조정해서 자신이 원하는 지표를 출력하도록 변형할 수 있습니다..! 저는 3가지를 출력하도록 했습니다. (실제 DNA 서열 간 거리와의 비교 시각화 / 상관계수^2 / R-squared)

evaluation_tree <- function(phylo){
  x <- as.vector(distance)
  y <- as.vector(as.dist(cophenetic(phylo)))
  plot(x, y, xlab = "original pairwise distances", ylab = "pairwise distances on the tree",
        main = "Algorithm", pch = 20, col = transp("black",.1), cex = 3)
  abline(lm(y~x), col = "red")
  cor <- cor(x, y)^2
  R2 <- R_2(x, y)
  print(cor)
  print(R2)
}

 *이 두 함수를 정의할 때 아래 링크의 코드를 모듈화했습니다.*

https://www.reconlearn.org/post/practical-phylogenetics.html

 

 bootvalue가 담긴 리스트를 만들고, 이를 기반으로 형성한 bootstrapped tree를 시각화&평가하는 과정입니다. 

boot.phylo의 parameter 중 주목할 부분은 function과 B입니다. function은 그냥 제 코드를 복붙하셔서 model과 out만 조정해주세요. B는 bootstrapping 횟수입니다. 기본적으로 NJ 계열 algorithm들은 2000번 정도로 설정해줍니다. default는 100입니다. parsimony는 말 그대로 parsimony score를 반환합니다. 곧 나올 maximum parsimony에서 설명할 것입니다. 지금은 단순히 작을수록 좋은 값이라고 여기세요. 이진트리만을 입력으로 받는 함수이기 때문에 bootstrapping 전 tree를 활용했습니다.

boot_bionj <- boot.phylo(tree_bionj_rooted, dna, function(e)
  root(bionj(dist.dna(e, model = "TN93")), out="CY013613"), B=2000)
tree_bionj_boot_rooted <- making_boot(tree_bionj_rooted, boot_bionj, 1400)
ggtree(tree_bionj_rooted) + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group])
evaluation_tree(tree_bionj_boot_rooted)
parsimony(tree_bionj_rooted, dna2)

 제 plot 결과도 첨부합니다. 

Plot restult 1

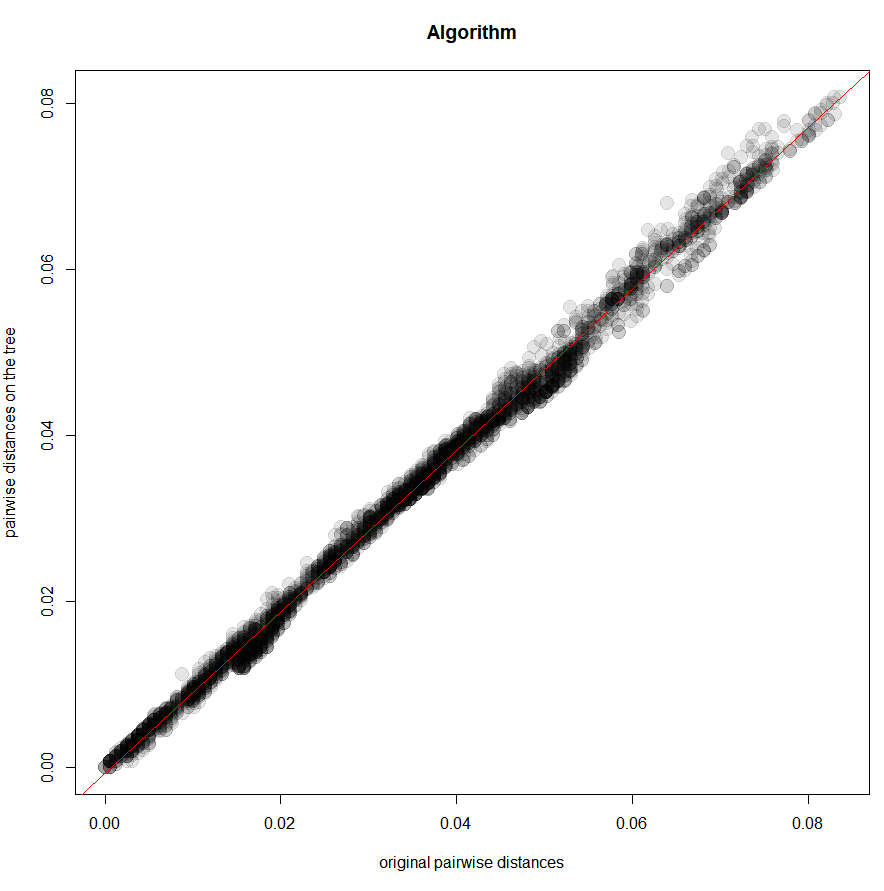
[1] 0.9955254
[1] 0.987024

다른 tree의 결과까지 종합하면 아래 표와 같습니다. UPGMA의 결과는 너무나 형편없어 아예 bootstrap도 하지 않았습니다.

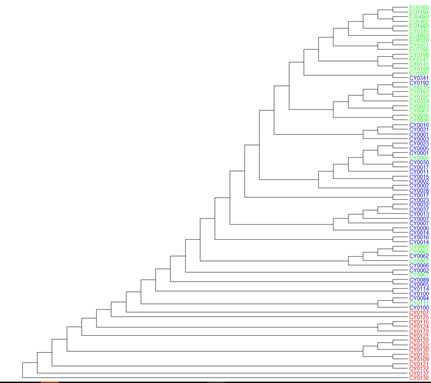
 이제 Maximum parsimony algorithm을 구현하겠습니다. (이 역시 개인적으로 딱히 좋아하는 알고리즘은 아닙니다. parsimony는 번역하면 "근검절약" 정도로 해석됩니다. 즉 maximum parsimony는 최대의 근검절약 정신을 실현하는 알고리즘입니다. 이 알고리즘은 각각의 염기변이를 한 형질로 간주하고, 이 형질 변이들의 합이 최소가 되도록 합니다. (원시형질, 파생형질 구분)

tree_nj_par <- optim.parsimony(tree_nj, dna2)
tree_bionj_par <- optim.parsimony(tree_bionj, dna2)
tree_prat <- pratchet(dna2)
tree_prat_rooted <- root(tree_prat, out = 4)
tree_nj_par_rooted <- root(tree_nj_par, out = 4)
ggtree(tree_nj_par_rooted) + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group])

 분명히 parsimony가 감소하였긴 했으나, 결과는 딱 봐도 영 형편없습니다. 따라서 그냥 넘어갔습니다. 

 

 세 번째로 Maximum Likelihood Algorithm을 구현하겠습니다. 개인적으로 굉장히 좋아하고, 실제로도 가장 많이 사용하는 알고리즘 중 하나입니다. long branch attraction 문제가 거의 나타나지 않으며 진화적 가설에도 적합합니다. 관측치를 바탕으로 parameter를 추정하는 방식으로, 이 친구 하나만으로 글을 쓸 수 있는 정도의 방대한 내용을 담고 있기에 이 글에선 생략하겠습니다. 추후 포스팅해보겠습니다.

 

 저는 가능한 거의 모든 경우의 수를 실현하는 함수 modelTest를 사용해 각종 parameter들을 채택했습니다. 

pmlmodels <- modelTest(dna2)
pmlmodels[pmlmodels$logLik==max(pmlmodels$logLik), "Model"]
env <- attr(pmlmodels, "env")
fit_GTR <- eval(get("GTR+G+I", env), env=env)
tree_pml <- fit_GTR$tree
ggtree(root(tree_pml, out=4)) + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group])

 

 또한 NJ 때와 마찬가지로 bootstrapping, evaluation을 수행했습니다. 코드가 약간 다르니 주의하세요. 여기서는 bootstrap.pml을 사용합니다. 또한 아까와 달리 시간 문제상, 100번만 수행했습니다. Maximum Likelihood는 100번 정도면 적당합니다. tree_pml_boot에는 이 역시 전과 다르게(아까는 리스트가 반환되었음) 100개의 트리가 저장되어 있기에 prop.clades로 value list를 추출해야 합니다. 그 후는 동일합니다. 다만 making_boot parameter의 stan을 70으로 변경했습니다. 이유는 아시겠죠?

tree_pml_boot <- bootstrap.pml(fit_GTR, optNni=T, bs=100)
boot_pml <- prop.clades(tree_pml, tree_pml_boot)
tree_pml_boot_rooted <- making_boot(tree_pml, boot_pml, 70)
evaluation_tree(tree_pml_boot_rooted)
parsimony(tree_pml, dna2)
ggtree(tree_pml_boot_rooted) + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group])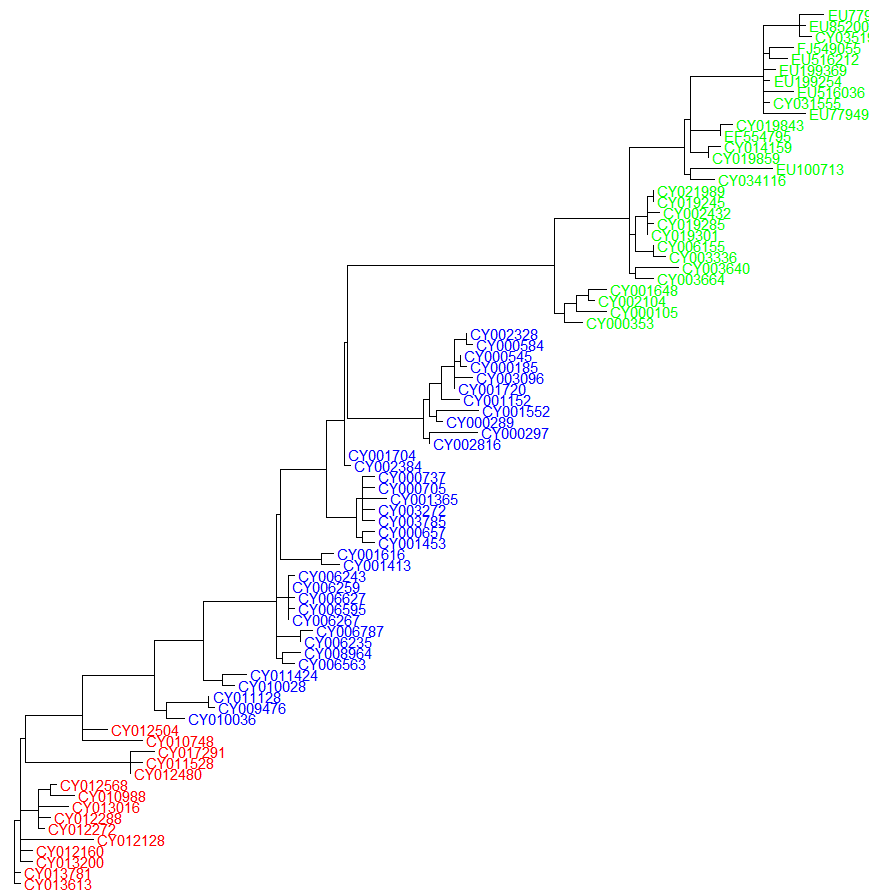 

 

 

 이제, 최종적으로 Phylogenetic Tree를 채택해야 합니다. pearson^2이나, R^2이나, parsimony 지표 모두 NJ가 BIONJ, ML에 비해 좋았습니다. 그러나 실질적 차이는 얼마 되지 않습니다. 0.01 정도라 오차범위 내에 들 듯하네요. 또한 모두Ancient H3N2, Old H3N2, New H3N2를 진화적으로 훌륭하게 분석했습니다.

 그러나 이때 pearson^2, R^2은 결국 distance에 기반해 계산된 것으로, NJ와 BIONJ가 ML보다 태생적으로 유리한 지표입니다. 추가적으로 long branch attraction에 대한 엄밀한 검증도 수행하지 않았으며 ML 자체가 특정 진화적 가설을 살피는 데에 매우 유리한 알고리즘임을 고려하여 ML을 택했습니다. 

 

*

보다 엄밀한 수학적 접근은 이 링크를 참고해주세요. tree clade 분석법 설명이 잘 되어있습니다. 게다가 한글 자료입니다.

http://amborella.net/2016-Bioinformatics/Week13-Chap4-2.pdf

 

 

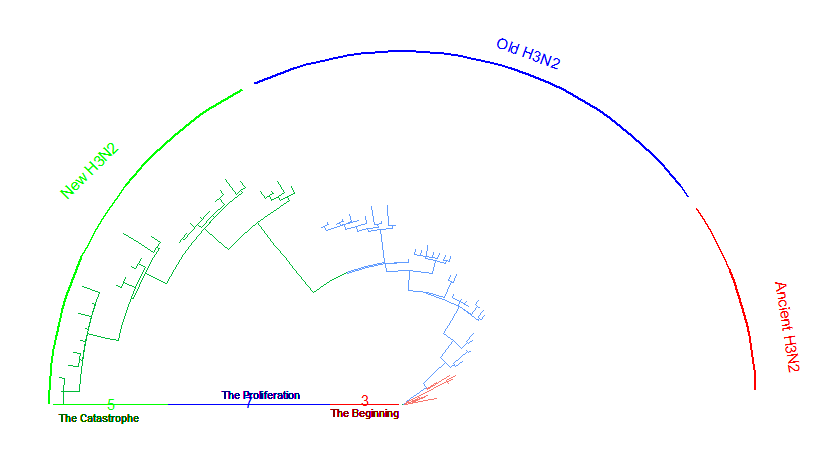
 아래 사진은 제가 모티브로 삼은 phylogenetic tree 시각화입니다.

 

 

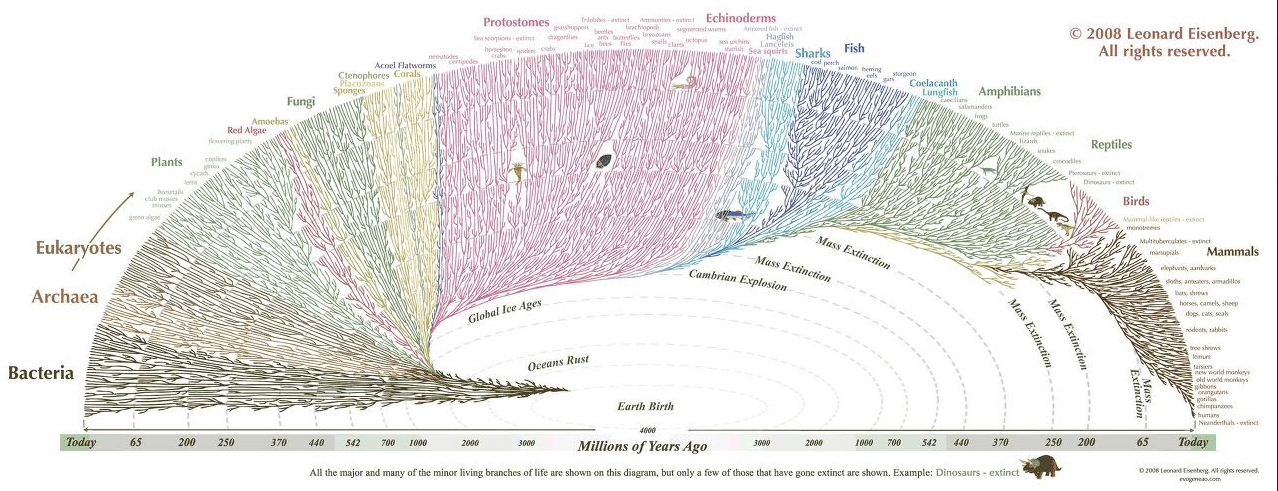
데이터가 80가지의 바이러스뿐이기에 저 정도로 방대한 양을 담지는 못하지만 최대한 비슷하게 시각화해보았습니다. 이 짧은 코드를 작성하기 위해 정말 많이 애썼습니다... ggtree로 구현하고자 하는 트리의 구조가 생각보다 잘 만들어지지가 않습니다. 특히나 타 패키지, 함수와 호환이 개떡같습니다. 게다가 제가 사용한 트리가 극좌표 기반이라 더욱 지원되지 않아 힘들었네요. 그래서 전 일단 직교좌표계로 구현한 후 극좌표로 변환하는 꼼수를 썼습니다. 

 

 먼저 코드를 살펴봅시다. 이 코드는 날짜를 맞춰주는 작업입니다. 위에서 만든 tree는 연도 반영이 되어있지 않습니다. 각 node 사이 거리가 상대적으로 나타나있기 때문에 이를 조정해주어야 합니다. 저는 Date2decimal 함수로 가장 이른 생명체와 늦은 생명체 사이 날짜를 수치로 변환해주었습니다. 또한 tree.age 함수로 root node인 CY013613과 가장 멀리 떨어져 있는 node 사이 거리를 알아냈습니다. 그리고 4번째 줄 코드로써 node 간 시간 반영을 완료했습니다. ggtree에 mrsd parameter와 theme_tree2()를 추가하면 mrsd의 날짜를 root node와 가장 멀리 떨어진 node의 x좌표로 한 x축을 출력합니다.

finaltree <- tree_pml_boot_rooted
Date2decimal("1993-01-01")
dispRity::tree.age(finaltree, order = "present")
finaltree$edge.length <- finaltree$edge.length*(2008-1993)/0.079

ggtree(finaltree, mrsd="2008-01-01") + geom_tiplab(as_ylab=TRUE, colour=c("red", "blue", "green")[annot$group]) + theme_tree2()

이렇게요! 이때 축을 좀 더 자세히 설정하고 싶으시다면 scale_x_continious function을 이용해보세요.

 

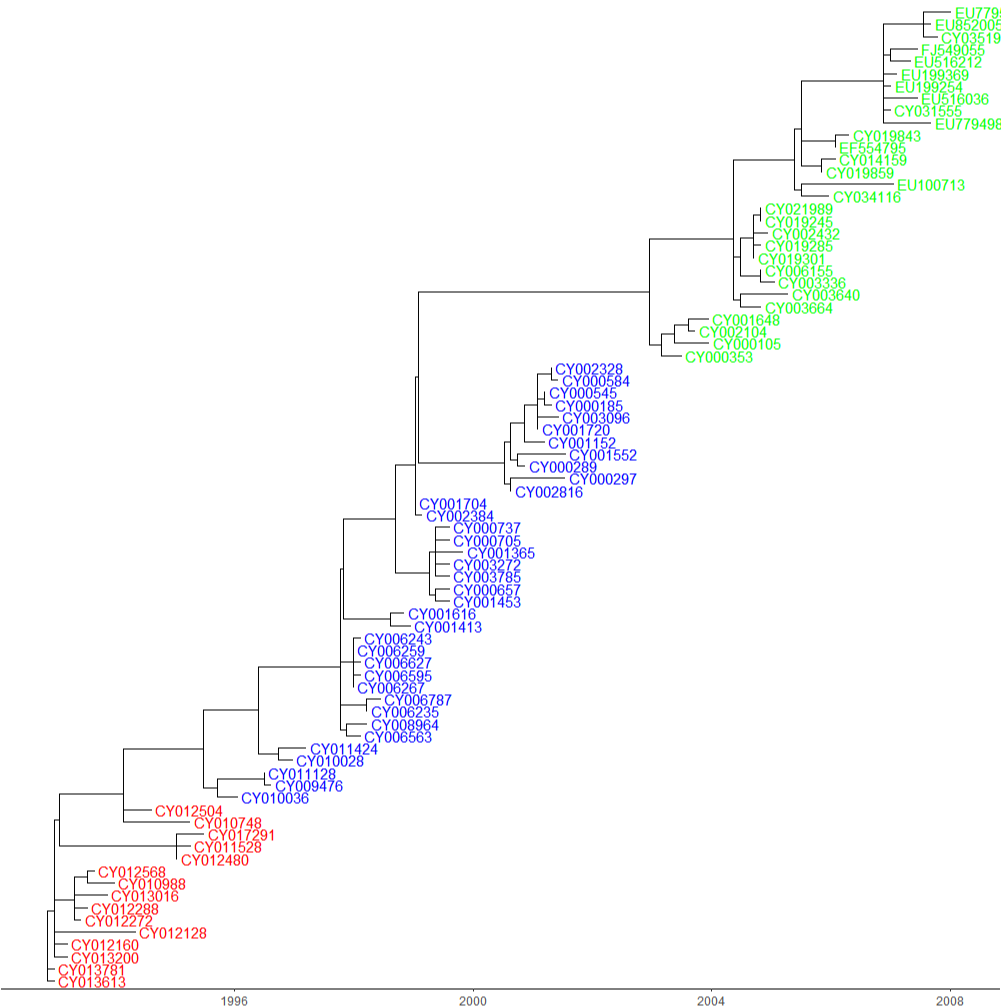
 그 후 이렇게 직교좌표계 기반 tree를 만들었습니다. 실제로 이렇게 만들어진 finalplot_tmp2를 plot해보면 굉장히 이상한 디자인이 나옵니다. 그 이유는 제가 이 tree를 극좌표로 변환한 다음, 극좌표 기반 tree의 디자인을 예쁘게 만들기 위해 파라미터를 조정했기 때문입니다. 실제로 해보셔야 감이 올 겁니다. 또한 모티브 tree처럼 기간에 이름을 정해주었습니다. (The beginning, The Proliferation, The Catastrophe = 시작, 대확산, 대재난 이게 무슨 코로나인가?)

 마지막 두 줄은 tree의 색깔을 group에 따라 바꿔주는 과정입니다.

finalplot_tmp2 <- ggtree(finaltree, mrsd="2008-01-01",size=0.5)

finalplot_tmp2 <- finalplot_tmp2 +
  geom_strip('EU779500', 'CY000353', barsize=1, color='green', label="New H3N2", offset.text=2, offset=-40, angle=45) +
  geom_strip('CY002328', 'CY010036', barsize=1, color='blue', label="Old H3N2", offset.text=1, offset=-40, angle=-20) +
  geom_strip('CY013613', 'CY012504', barsize=1, color='red', label="Ancient H3N2", offset.text=2, offset=-40, angle=-81) +
  geom_treescale(x=1993, y=80, width=3, color="red") +
  geom_treescale(x=1996, y=80, width=7, color="blue") +
  geom_treescale(x=2003, y=80, width=5, color="green") +
  geom_text(x=1994.5, y=85, label="The Beginning", size=3, color="darkred") +
  geom_text(x=1999, y=78, label="The Proliferation", size=3, color="darkblue") +
  geom_text(x=2006, y=81, label="The Catastrophe", size=3, color="darkgreen")

grp <- list(Ancient_H3N2=annot[annot$group==1, "accession"], Old_H3N2=annot[annot$group==2, "accession"], New_H3N2=annot[annot$group==3, "accession"])
finalplot_tmp2 <- groupOTU(finalplot_tmp2, grp, "Virus") + aes(color=Virus) + theme(legend.position = "none")

 극좌표계 변환은 간단합니다. 전 open_tree를 활용했습니다. 두 번째 파라미터는 열린 각입니다. 이 역시 직접 바꿔가며 해보셔야 아실 겁니다. 이를테면 저는 반원 모양을 만들려 했기 때문에 180도를 열어놨습니다. 

finalplot <- open_tree(finalplot_tmp2, 180) + theme(axis.title.y=element_blank())
finalplot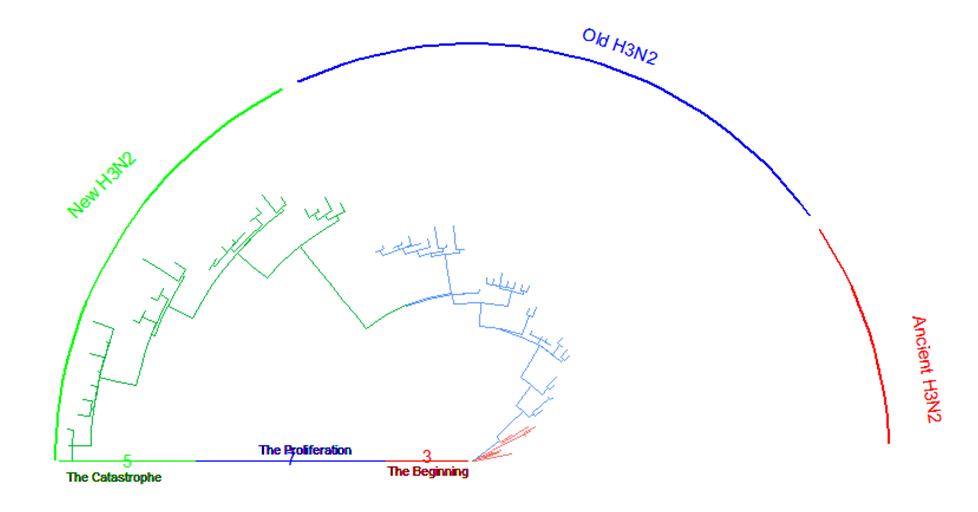

 여기서 글을 마치겠습니다. 지금까지 쓴 글 중 가장 길었네요. 이 글에 독자들이 phylogenetic tree를 그리는 데에 있어서 참고할 만한 내용이 담겨있길 바랍니다. rython 블로그였습니다.

 

Written By Killer T Cell