Phylogenetic Tree(계통수) 실습 in R (1) - DNA Alignment, Hierarchical Clustering, Multidimensional Scaling

안녕하세요, Killer T Cell입니다. 이번에는 Phylogenetic Tree를 R로써 어떻게 구현하는지 포스팅하겠습니다. 전체적 개괄은 다음과 같습니다.

 

우선 Phylogenetic Tree란 생물의 진화로 인해 발생한 유사성, 차이를 기반으로 친연 관계를 분석해 그림으로 나타낸 일종의 다이어그램입니다. 각 node 간의 수직적 거리가 진화적 거리를 의미하며, 이외에도 여러 주요한 특징이 있으나 이곳은 R 카테고리이기에 자세한 내용은 생략하겠습니다. 이 글을 보시는 분들은 이미 충분히 배경에 대해 아시라 생각합니다...^^

 

사용한 DATASET입니다. 

Source: https://www.ncbi.nlm.nih.gov/genbank/ 

usflu.annot.csv

0.00MB

usflu.fasta

0.13MB

A형 influenza를 일으키는 H3N2 virus의 sequence data입니다. 발견 연도와 장소가 csv에 기재되어 있습니다.

이제 본격적으로 시작해보겠습니다.

일단 사용할 패키지들을 library해줍시다. 일부 패키지의 경우 install.packages로 되지 않는데, 이 경우 <package 이름> download 라 검색하시면 쉽게 해결하실 수 있습니다.

library(ape)
library(ade4)
library(adegenet)
library(phangorn)
library(ggtree)
library(cluster)
library(factoextra)
library(ggplot2)
library(treeio)
library(tibble)
library(msa)
library(doParallel)
library(phytools)

 

사용할 data를 불러왔습니다. 이때 dna, dna2가 공존하는 이유는 각 패키지가 요구하는 데이터 형식이 달라 같은 정보를 담는 다른 데이터 구조가 필요하기 때문입니다. ^^

registerDoParallel(detectCores())
setwd("C:/Tree of Life")
dna <- fasta2DNAbin(file = "usflu.fasta") #virus file
dna
annot <- read.csv("usflu.annot.csv",
                  header = TRUE, row.names = 1, stringsAsFactors = FALSE)

dna2 <- readDNAStringSet("C:/usflu.fasta")

 

우선 어떤 DNA data든 간에 alignment를 필요로 합니다. 아래는 alignment를 간단히 요약한 그림입니다.

MIT 강의자료 발췌

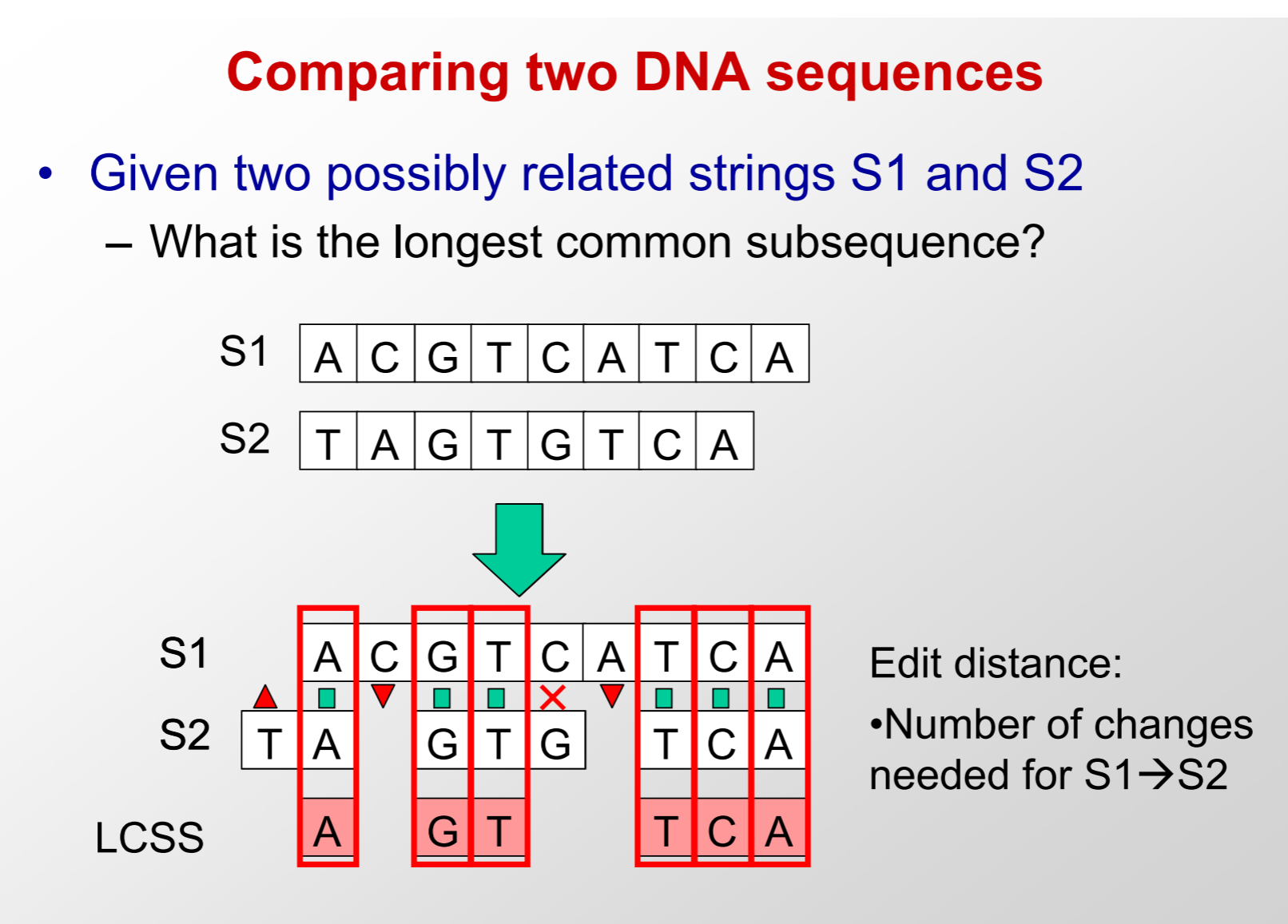
DNA mutation 과정에서 결실, 삽입이 발생하기 때문에 각 base를 정렬하며 유사성을 최대한 맞춰주는 과정으로 생각하시면 됩니다. 향후 모든 데이터는 반드시 alignment된 채로 활용되어야 하기에 여기에서도 진행해주었습니다.

과정은 간단합니다. msa function을 사용하시면 되는데, 이때 algorithm은 잘 선택하셔야 합니다.

msa function이 제공하는 algorithm들은 'Muscle', 'ClustalW', 'ClustalOmega'입니다. Muscle은 비교적 많은 분류군에 적합하며 빠르게 분석하면서 높은 정확성을 보입니다. (많은 교수들이 Muscle을 선호하는 듯합니다.) 한편 ClustalOmega는 이보다 조금 느리지만 분류군의 크기와 관계없이 적합한 알고리즘입니다. 반면 ClustalW는 적은 분류군에만 사용이 제한되어 있습니다. 관련 링크를 첨부해드립니다.

https://help.geneious.com/hc/en-us/articles/360044627712-Which-multiple-alignment-algorithm-should-I-use-

https://www.researchgate.net/post/Which_program_is_the_best_for_multiple_sequence_alignment_nowadays 

 

어쨌든 저는 Muscle을 사용했습니다! dna_msa의 형태를 적합하게 변환하고 image function으로 이를 시각화하였고,  dna_msa를 dna에 다시 저장하였습니다. (사실 이 데이터는 이미 alignment된 상태로 추정되네요! ^^)

dna_msa <- msa(dna2, "Muscle")
dna_msa <- as.DNAbin(dna_msa)
image(dna)
image(dna_msa)

dna <- dna_msa[rownames(dna),]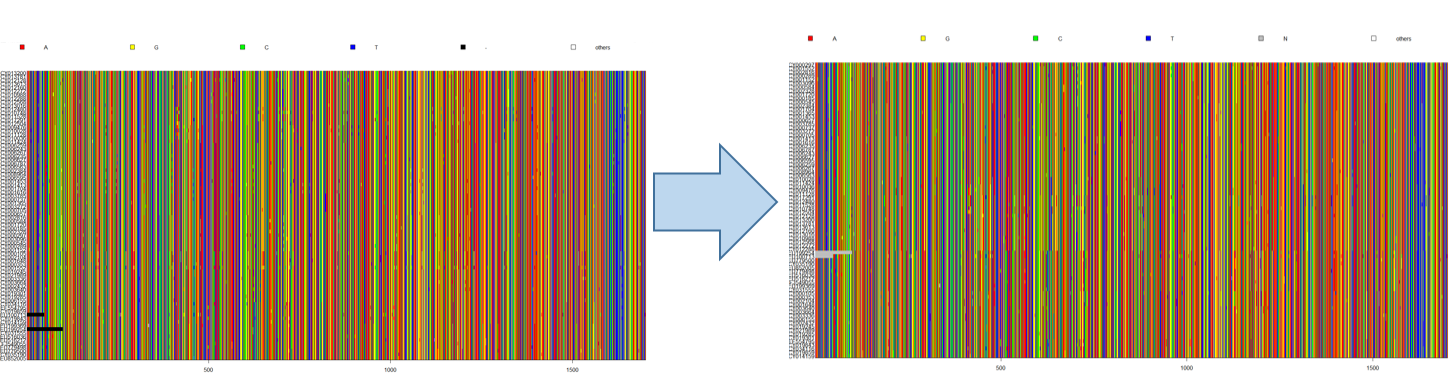

Alignment 결과

앞서 언급하였지만 Hierarchical Clustering을 차후 진행할 것이고, 그 외에도 distance based algorithm들을 활용해야 하기 때문에 virus 간 distance(서열 유사도로 생각하시면 편합니다.)를 계산해야 합니다. 저는 dist.dna function을 사용했습니다. 이때 model 선택을 조금 신중히 해야 합니다. dist.dna가 지원하는 모델들을 열거해보겠습니다. 

 "RAW" "JC69" "K80" "F81" "K81" "F84" "T92" "TN93" "GG95" "LOGDET" "BH87" "PARALIN" "N" "TS" "TV" "INDEL" "INDELBLOCK"

각 모델들을 일일이 설명할 수 없기에.. ?dist.dna 를 치시고 모델 설명을 보는 것을 권장합니다. 위키피디아 링크도 첨부해드립니다. 다만 저는 TN93을 선호합니다. transition/transversion 구분, different base frequency,

different between-site variation of the substitution rate 등이 매력적으로 느껴졌네요.

https://en.wikipedia.org/wiki/Models_of_DNA_evolution 

table.paint로 각 거리를 밝고 어두운 정도로 나타낼 수 있습니다. 참고만 하세요! 밝을수록 가까운 거리를 의미하고, 이를 바탕으로 뭔가 구분되는 듯한 느낌을 받으실 수 있을 겁니다. 만약 유전적 거리가 멀다고 알려져 있는 두 개체나 두 분류군이 있다면 이를 기반으로 distance의 결과를 판단할 수 있겠죠?

distance <- dist.dna(dna, model="TN93") #distance of DNA sequences

mat <- as.data.frame(as.matrix(distance)) 
table.paint(mat, cleg = 0, clabel.row = .5, clabel.col = .5)

table.paint 결과

지금 설명할 부분은 분자시계입니다. 이 글을 보시는 모든 분들이 분자시계를 사용할 필요가 있지는 않습니다. 부적절한 경우가 충분히 발생할 수 있는데, 이를 검증하는 법도 첨부하겠습니다. 

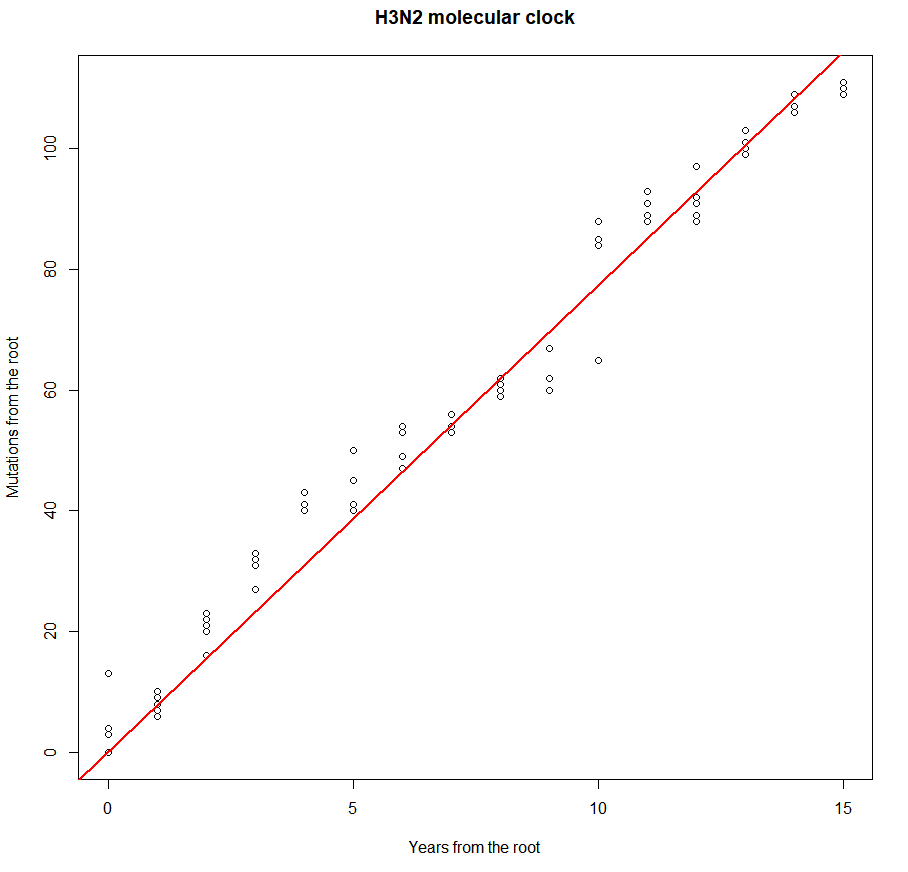
우선 mutation matrix를 첫 줄과 같이 생성합니다. [1, ]는 기준 생명체가 1번이라 지정하는 것으로, 이에 대해서는 후술하겠습니다. 제 데이터의 경우 발견 연도가 명확해 year 객체처럼 기준 생명체로부터 발견된 시간을 계산할 수 있습니다. 일단 이를 plot하였을 때 선형적 관계가 나타난다면 성공입니다. 더 구체적으로 보기 위해 선형회귀 결과를 저장한 clock 객체를 만들고, 직선을 그어주었습니다. clock 객체가 어떻게 만들어지는지 궁금하시다면 이 블로그의 다른 글을 참고해주세요. 링크 첨부해드립니다.

https://rython.tistory.com/2

다중회귀분석 실습

mutation <- as.matrix(dist.dna(dna, model = "N"))[1,] #molecular clock
year <- annot$year - annot$year[1]
par(mar=c(5,6,4,1)+.1)
plot(mutation ~ year, xlab = "Years from the root", ylab = "Mutations from the root", main = "H3N2 molecular clock")
clock <- lm(mutation ~ -1 + year)
summary(clock)
abline(clock, col = "red",lwd = 2)

저 글의 내용을 잘 숙지하셨다는 가정 하에 계속 서술하겠습니다. 이 데이터의 경우 plot, summary 시 아래와 같이 출력됩니다.

Call:
lm(formula = mutation ~ -1 + year)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.327  -1.577   1.004   6.386  13.000 

Coefficients:
     Estimate Std. Error t value Pr(>|t|)    
year  7.73274    0.07443   103.9   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.86 on 79 degrees of freedom
Multiple R-squared:  0.9927,	Adjusted R-squared:  0.9926 
F-statistic: 1.079e+04 on 1 and 79 DF,  p-value: < 2.2e-16

R^2이 0.9927로 상당히 높으나 이 값이 최고치라고 보장할 수 없습니다. 즉 기준 생명체를 변경한다면 더 높아질 수 있습니다. 이 데이터는 가장 오래 전에 발견된 바이러스가 1993년 발견 5종입니다. 그러나 구체적 날짜가 공개되어 있지 않기에 5종을 모두 동일한 코드로 테스트하였고(앞서 서술했듯 [1, ]를 [2, ] 또는 [3, ] 등으로 바꾸었습니다.), 그 결과 4번째 바이러스인 CY013613을 root로 확립하였습니다. (R^2=0.9933) 만약 R^2이 현저하게 낮다면 (대략 0.7 미만) 다른 방법을 취하시는 것을 권장합니다!! root를 확립하여야 차후 phylogenetic tree를 그릴 때 용이합니다. 물론 분자시계를 활용하지 않아도 root 확립에 방법은 있습니다. 참고할 수 있는 링크를 2편에 달아드릴게요. (지금 1편의 내용은 phylogenetic tree를 효과적으로 뒷받침할 수 있는 다른 체계적 방법들을 사용하는 것입니다. 이 방법이 아닌 다른 root 확립법은 2편에서 tree를 그리고 추론해야 합니다.)

 

2021/1/29 수정

다만 이런 방법이 옳지는 않습니다. 현재 수행한 outgroup rooting은 여타 생명체들과 진화적으로 거리가 먼 생명체를 outgroup으로 잡는 방식인데, 제 경우 이를 가장 먼저 출현했을 것으로 추정되는 공통조상으로 잡았습니다. 따라서 이 부분은 크게 참고하지 않으셔도 됩니다.

 

다음으로 Hierarchical clustering(계층적 군집분석)입니다. 사실 비지도학습은 다른 카테고리에 서술해야 하지만 독자들의 편의를 위해 여기에도 연재합니다. clustering만을 다루는 글은 unhierarchical clustering까지 이론적으로도 다뤄보도록 하죠..^^

저는 Hierarchical clustering을 사용하였지만 unhierarchical clustering을 사용하셔도 무방합니다. 그러나 조금 번거로울 수는 있습니다. 더 깊게 들어가자니 독자들의 혼란만 가중시킬 것 같아 생략하겠습니다! 향후 clustering 글을 작성하면 링크 올려놓겠습니다.

 

들어가기 전, 이 사실을 반드시 기억하고 또 주의하세요. Hierarchical clustering으로 tree를 그릴 수는 있습니다. 그러나 이것은 절대 phylogenetic tree로 결정지어선 안 됩니다. clustering을 통한 phylogenetic tree는 UPGMA로 불리는 알고리즘을 사용합니다. 즉 method="Average"를 사용합니다. 이때 이 알고리즘에 여러 문제가 존재하는데, 대표적으로 생선 -> 원숭이 -> 인간으로 진화했어도 실제로 그려지는 tree에서 원숭이 -> 인간 -> 생선이라고 나타날 가능성이 있습니다. 그럼에도 불구하고 clustering의 결과가 생선, 인간, 원숭이를 명확히 구분해주기 때문에 이 과정을 거치는 것입니다. 한 마디로 말해서, 이 결과가 올바른 phylogenetic tree가 아닐 수는 있으나 cluster는 명확히 구분합니다.

 

코드 자체는 심플합니다. hclust function의 method parameter를 single, complete.etc로 바꿔가며 다양한 hclust 객체를 생성할 수 있습니다. 문제는 여기서 어떤 tree를 선택하냐는 것이지요...

hc <- hclust(distance, method = "ward.D2") #single, complete, ward.D2, average, centroid

plot(as.dendrogram(hc))

일단 plot 결과를 아래 사진에 담았습니다.

 

우리가 최적의 군집을 택하기 위해 고려할 점은 "연결법(method)"과 "군집의 수", "군집 tree의 생김새"입니다. 희한해보이지만 군집 tree의 생김새가 중요합니다. 어느 정도 균일하게 섞였는지, branch가 긴지 등을 고려하는 경우가 많습니다. 일단 이 글에서는 정량적 지표인 silhouette coefficient와 정성 평가로만 clustering 결과를 확립하였습니다. (clustering의 경우 R-squared, accuracy 등의 명백한 평가 지표가 없어요 ㅠㅠ.. 따라서 어느 게 좋다고 딱 잘라 말하기 어렵습니다.)   

 

method를 달리하며 hc를 다르게 만들고, k(cluster의 수)를 조정해가며 최고값을 찾는 과정을 수행하는 코드입니다. 제가 k=2, k=3, k=4로 설정한 이유는 위 사진에서 군집을 나누었을 때 3개 정도로 나누면 적당할 것으로 생각했기 때문으로 각자 데이터의 결과에 맞게 k를 바꿔가시면 되겠습니다.

plot(silhouette(cutree(hc,k=2),dist=distance,col=1:2)) #decision of number of clusters, more imformation in PPT
plot(silhouette(cutree(hc,k=3),dist=distance,col=1:3))
plot(silhouette(cutree(hc,k=4),dist=distance,col=1:4))

plot 결과는 이렇게 나옵니다.

1에 가까운 값은 그 개체가 특정 군집에 적절히 포함되어 있음을 의미합니다. 여기서는 3개의 개체가 음수로 오히려 부적절하게 군집화되었음을 알 수 있네요. Anyway, 제일 중요한 지표는 아래의 Average silhouette width로 0.62가 계산되었네요. 이 값을 체크해서 표로 만들어보았습니다.

 

Silhouette coefficent 표

최고값을 보인 최소연결법, 와드연결법(k=3) 트리를 비교하였을 때 와드연결법의 branch가 더 길고, 생김새도 매우 자연스럽기에 최종적으로 와드연결법(k=3) model을 택했습니다.

이를 예쁘게 plot해봤습니다.

fviz_dend(hc, palette = "jco", k=3, k_colors=c("blue", "red", "green3"), #visualizaiton
          rect = F, show_labels = TRUE, lwd=0.8)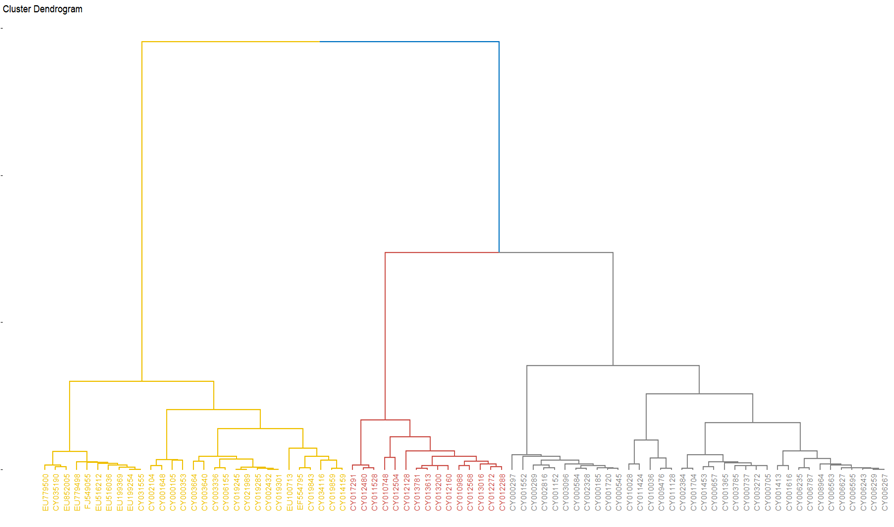

그리고 이 clustering 결과를 기존 dataframe과 연계했습니다.

cut <- cutree(hc, k=3)

group1 <- cut[cut==1]
group2 <- cut[cut==2]
group3 <- cut[cut==3]

annot[annot$accession %in% names(group1), "group"] <- 1 
annot[annot$accession %in% names(group2), "group"] <- 2
annot[annot$accession %in% names(group3), "group"] <- 3

 

여기에서 그치지 않고 각 cluster를 naming했습니다. (불필요한 부분이라 지나가실 분은 지나가셔도 돼요!) 전 이렇게 연도별로 군집화가 이루어져 있음을 확인하고 각 군집을 Ancient H3N2, Old H3N2, New H3N2로 명명했습니다!

*아까 생선, 원숭이, 인간의 예시로 설명한 현상이 여기서도 나타나고 있습니다*

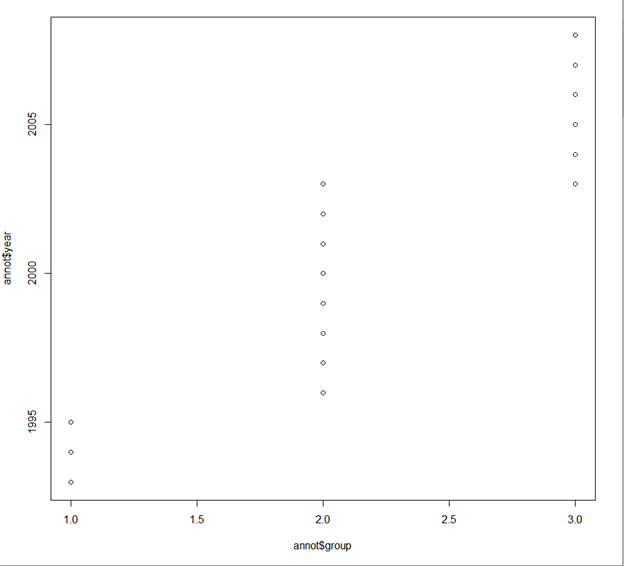
plot(annot$group, annot$year)

 

1편의 마지막 부분, Multidimensional Scaling(MDS)입니다. 다차원의 데이터를 저차원으로 시각화하는 방법으로, PCA와 유사한 부분이 있습니다. 그러나 PCA는 euclidean distance에만 적합하기 때문에 MDS를 사용하겠습니다. 코드가 몹시 길어보이지만 실질적으로 첫 줄만이 중요합니다. ggplot 부분은 단순히 제가 시각화를 위해 여러가지 파라미터를 달아준 코드입니다.

 

예쁘게 되었네요!

mds <- cmdscale(distance)
ggplot(as.data.frame(mds), mapping=aes(x=V1, y=V2)) + 
  geom_point(colour=c("red", "blue", "green")[annot$group]) +
  annotate("rect", xmin= -0.03, xmax=0, ymin=-0.0025, ymax=0.025, fill="skyblue", alpha=0.5) +
  annotate("rect", xmin= -0.05, xmax=-0.025, ymin=-0.017, ymax=-0.01, fill="pink", alpha=0.5) +
  annotate("rect", xmin= 0.017, xmax=0.045, ymin=-0.01, ymax=0.006, fill="green", alpha=0.2) +
  annotate("text", x=-0.0375, y=-0.0085, label="Ancient H3N2", size=6) +
  annotate("text", x=-0.015, y=-0.004, label="Old H3N2", size=6) +
  annotate("text", x=0.031, y=-0.011, label="New H3N2", size=6)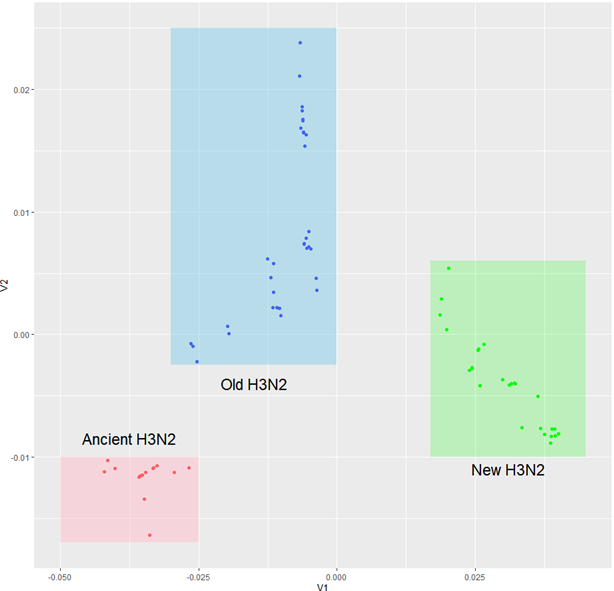

 

이제 여기에서 글을 마치겠습니다. 저희는 DNA alignment로 데이터를 가공하였고, 각 생명체들을 clustering으로 군집화했으며 이를 MDS로 시각화했습니다. 이제 phylogenetic tree를 그리기 위한 모든 준비가 다 되었네요. 2편에서는 실제로 이 tree를 그리기 위해 사용하는 알고리즘들을 R로 구현하고, 또 평가한 뒤에 예쁘게 시각화해보겠습니다. 긴 글 읽어주셔서 감사합니다. 

 

2편 링크입니다!

https://rython.tistory.com/11

Phylogenetic Tree(계통수) 실습 with R (2) - Neighbor Joining, Maximum parsimony, Maximum Likelihood, Bootstrapping, ggtree

 

Written By Killer T Cell